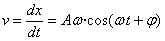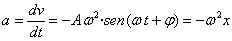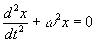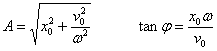FLUIDOS

FLUIDOS

Fluidos

---

Se entiende por fluido todo cuerpo cuyas moléculas tienen entre sí poca coherencia y toma siempre la forma del recipiente donde está contenido. Dentro de esta definición los fluidos se consideran a la materia en estado líquido y gaseoso. El estado líquido se ve, pero el estado gaseoso es más difícil de ver e identificar .

Una de las magnitudes físicas que pueden hacer más factibles la existencia del estado gaseoso, es la presión (del latín pressio, -onis) acción y efecto de apretar o comprimir; que es la distribución o “propagación de una fuerza”, es decir no solamente fuerza, sino fuerza sobre algo más. Exactamente la presión se define como fuerza sobre la unidad de área.

Para dar las unidades de la presión hay que tener en cuenta las magnitudes con que se relaciona, es decir fuerza y superficie.

En el Sistema Internacional es el Newton dividido entre el metro cuadrado, y recibe el nombre de Pascal (Blaise Pascal –1623-1662, matemático, físico, filósofo francés).

1 Pa =  1 N/m²

Pero en los comprensores de las estaciones de servicio, lo que nos encontraremos son los  kilos por centímetro cuadrado.

ACTIVIDAD 1.- MIRA ATENTAMENTE LAS DOS PRESENTACIONES : FLUIDOS EN REPOSO Y FLUIDOS EN MOVIMIENTOS DEL LIBRO DE TIPPENS Y ELABORA UN CUADRO COMPARATIVO , ENVIA.

Fluidos en reposo from angelica_ma_cc

Tippens fisica 7e_diapositivas_15b from votrefolie


CONCEPTOS IMPORTANTES
1.-Fluidos en reposo (Hidrostática): Son todos aquellos cuerpos que tienen la característica de ser líquidos o gaseosos, tener la forma del recipiente que los contiene y tener viscosidad.
2.-Presión absoluta: Es la fuerza ejercida sobre la superficie en todas direcciones.
3.-Presión relativa: Es la fuerza aplicada sobre una superficie en una o más direcciones sin llegar a ser total.
4.-Presión atmosférica: Es la presión ejercida sobre todos los objetos de la tierra por la capa de varios kilómetros de altura, que envuelve nuestro planeta.
5.-Barómetro de Torricelli: Aparato que sirve para medir la presión atmosférica. Consiste en un tubo de vidrio lleno de mercurio invertido sobre una cubeta con este mismo líquido; por la parte superior se tapa el orificio y al destaparlo se observa que al nivel del mar se crea un vacío igual a 760 mm. El resultado indica que lo que sostiene a dicha columna de mercurio en el interior del tubo, es la presión atmosférica.
  6.-Manómetro de tubo en U: Es un aparato que sirve para medirla presión de un gas contenido en un recipiente, se basan en el mismo principio que los barómetros, pudiendo ser metálicos como los aneroides o hidrostáticos.
La diferencia de alturas (h) indica la presión manométrica del gas contenido en el tanque.
Pm=Pa
sm=kg/m3
h=m
g=9.81 m/s2
Pm=sgh


7.-EJEMPLO DE PROBLEMA DE APLICACIÓN:
A.-Determinar la presión de un gas contenido en un manómetro que tiene de densidad 1.33 kg/m' y alcanza una altura de 1.5 m.
Pm=dgh
Pm=(1.33 kg/m3)(9.81 m/s2)(1.5 m)=13.04 Pa

8.-Principio de Pascal: Al aplicar una presión exterior en un punto de un fluido (líquido o gas) confinado en un recinto, la presión en cada punto del mismo aumenta en una cantidad igual a la citada presión exterior, esto quiere decir, que la presión ejercida en un punto es igual en todas direcciones.
F= fuerza mayor
A=área mayor
f=fuerza menor
a=área menor
F/A=f/a

9.-EJEMPLO DE PROBLEMA DE APLICACIÓN: En una prensa hidráulica existe una presión de 2.5 Pa en una área de 3 m2 en el émbolo de mayor tamaño, ¿Cuál será la fuerza que existe en el émbolo de menor tamaño, si su tamaño es 3 veces menor?


A.-Primero se determina la fuerza que existe en el primer émbolo.
P=F/A               F=PA=(2,5 Pa)(3m2)=7.5 N
B.-Con estos valores sustituimos en la fórmula del Principio de Pascal y tenemos:

F= 7.5 N                      A=3 m2       f=x          a=1 m2          f=Fa/A      
f=Fa/ A=(7.5 N)(1 m2)/3 m2=2.5 N 

10.-Prensa hidraúlica: Este aparato se encuentra formado por un recipiente completamente lleno de algún líquido con dos émbolos de área diferente. Si en el émbolo más pequeño se ejerce una fuerza, el liquido recibe la presión al mismo tiempo sobre el émbolo más grande debido a la fuerza que se produce.
11.-Principio de Arquímedes: Todo cuerpo total o parcialmente sumergido en un fluido experimenta un empuje hacia arriba (por parte del fluido) igual al peso del volumen del fluido que desaloja, en otras palabras, un cuerpo sumergido en un fluido experimenta una pérdida de peso aparente igual al peso del fluido que desaloja.
La dirección del empuje (fuerza) se considera vertical con sentido hacia arriba y aplicado en el centro de gravedad del fluido desplazado.
Empuje = Peso del fluido desalojado
12.-Fuerza de flotación o empuje: Es igual al peso del fluido desalojado por el recipiente y se calcula con la siguiente fórmula:
E=N
Pv=N/m3
 V=m3
 E=PvV
13.-EJEMPLO DE PROBLEMA DE APLICACIÓN:
Determinar la presión que ejerce un barco en el agua si el empuje del mismo en una cierta área es de 123 N y el volumen es de 20 m3.

E=PvV por lo que Pv=E/V
Pv=123 N/20 m3=6.15 N/m3

14.-Presión hidrostática: Es la debida a la columna de un fluido de altura h y densidad de masa r (o densidad de peso D):
P= h rg= h D
15.-Tensión superficial: Fenómeno por el cual un líquido tendrá rigidez en la capa superficial, debido a que las moléculas que se encuentran en su interior están sometidas en todas direcciones y por igual. 16.-Capilaridad: Fenómeno que consiste en la propiedad de los líquidos de ascender o descender por tubos capilares.

ACTIVIDAD 2.- RESUELVE LOS SIGUIENTES PROBLEMAS


Consideremos el movimiento de un objeto de volumen V y masa M que cae a través de un fluido con viscosidad cero (sin rozamiento).

• Dibuja las fuerzas que actúan sobre el cuerpo.
• ¿La aceleración del objeto en caída es independiente de su masa?, ¿y de su volumen?

Disponemos de una plancha de corcho de 1 dm de espesor. Calcular la superficie mínima que se debe emplear para que flote en agua, sosteniendo a un naúfrago de 70 kg. La densidad del corcho es de 0.24 g/cm2.
Nota: entendemos por superficie mínima la que permite mantener al hombre completamente fuera del agua aunque la tabla esté totalmente inmersa en ella.

Un cable anclado en el fondo de un lago sostiene una esfera hueca de plástico bajo su superficie.El volumen de la esfera es de 0.3 m3 y la tensión del cable 900 N.

• ¿Qué masa tiene la esfera?
• El cable se rompe y la esfera sube a la superficie. Cuando está en equilibrio, ¿qué fracción del volumen de la esfera estará sumergida?.

Densidad del agua de mar 1.03 g/cm³

Un depósito de agua está cerrado por encima con una placa deslizante de 12 m2 y 1200 kg de peso. El nivel del agua en el depósito es de 3.5 m de altura. Calcular la presión en el fondo. Si se abre un orificio circular de 5 cm de radio a medio metro por encima del fondo, calcúlese el volumen de agua que sale por segundo por este orificio. (Se considera que el área del orificio es muy pequeño frente al área del depósito).

Dato: la presión atmosférica es de 10⁵ Pa

La prensa hidráulica de la figura está formada por dos depósitos cilíndricos, de diámetros 10 y 40 cm respectivamente, conectados por la parte inferior mediante un tubo, tal como se indica en la figura. Contienen dos líquidos inmiscibles: agua, de densidad 1 g/cm3 y aceite 0.68 g/cm3. Determinar el valor de la masa m para que el sistema esté en equilibrio. Tomar g=9.8 m/s2. Presión atmosférica = 101293 Pa.

El depósito de la figura contiene agua. a) Si abrimos la llave de paso, ¿qué altura tendrá el agua en cada lado del depósito cuando se alcance el equilibrio? b) ¿qué cantidad de agua pasará de un recipiente al otro hasta que se alcance el equilibrio?

De un gran depósito de agua, cuyo nivel se mantiene constante fluye agua que circula por los conductos de la figura hasta salir por la abertura D, que está abierta al aire. La diferencia de presión entre los puntos A y B es PB - PA = 500 Pa.

Sabiendo que las secciones de los diferentes tramos de la conducción son S_A= S_C = 10 cm² y S_B=20 cm², calcular las velocidades y las presiones del agua en los puntos A, B, C, de la conducción.

La presión en C es la atmosférica, igual a 10⁵ Pa.

Para saber la velocidad del agua en una tubería empalmamos en ella un tubo en forma de T de menor sección, colocamos tubos manométricos A y B, como indica la figura y medimos la diferencia de altura (5 cm) entre los niveles superiores del líquido en tales tubos. Sabiendo que la sección del tubo estrecho es 10 veces menor que la tubería, calcular la velocidad del líquido en ésta. Calcúlese el gasto, si el área de la sección mayor es 40 cm2

El gasto en una tubería por la que circula agua es 208 l/s. En la tubería hay instalado un medidor de Venturi con mercurio como líquido manométrico. Si las secciones de las tuberías son 800 y 400 cm2,Calcular el desnivel h que se produce en el mercurio. Dato: densidad del mercurio 13.6 gr/cm3

Dos depósitos abiertos muy grandes A y F, véase la figura, contienen el mismo líquido. Un tubo horizontal BCD que tiene un estrechamiento en C, descarga agua del fondo del depósito A, y un tubo vertical E se abre en C en el estrechamiento y se introduce en el líquido del depósito F. Si la sección transversal en C es la mitad que en D, y si D se encuentra a una distancia h1 por debajo del nivel del líquido en A.¿A qué altura h2 alcanzará el líquido en el tubo E?. Expresar la respuesta en función de h1.

Del depósito A de la figura sale agua continuamente pasando través de depósito cilíndrico B por el orificio C. El nivel de agua en A se supone constante, a una altura de 12 m sobre el suelo. La altura del orificio C es de 1.2 m. El radio del depósito cilíndrico B es 10 cm y la del orificio C, 4 cm. Calcular: §         La velocidad del agua que sale por el orificio C. §         La presión del agua en el punto P depósito pequeño B §         La altura h del agua en el manómetro abierto vertical. Dato: la presión atmosférica es 101293 Pa.

MOVIMIENTO ARMÓNICO SIMPLE

El estudio del oscilador armónico constituye en Física un capítulo muy importante, ya que son muchos los sistemas físicos oscilantes que se dan en la naturaleza y que han sido producidos por el hombre.

Movimiento armonico simple from Moisés Galarza Espinoza

Definición

Una partícula describe un Movimiento Armónico Simple (M.A.S.) cuando se mueve a lo largo del eje X, estando su posición x dada en función del tiempo t por la ecuación

x=A·sen(ωt+φ)

donde

• A es la amplitud.
• w la frecuencia angular.
• w t+j la fase.
• j la fase inicial.

Las características de un M.A.S. son:

• Como los valores máximo y mínimo de la función seno son +1 y -1, el movimiento se realiza en una región del eje X comprendida entre -A y +A.

• La función seno es periódica y se repite cada 2p, por tanto, el movimiento se repite cuando el argumento de la función seno se incrementa en 2p, es decir, cuando transcurre un tiempo P tal que w(t+P)+j=w t+j+2p .

P=2π/ω

Cinemática de un M.A.S.

En un movimiento rectilíneo, dada la posición de un móvil, obtenemos la velocidad derivando respecto del tiempo y luego, la aceleración derivando la expresión de la velocidad.

La posición del móvil que describe un M.A.S. en función del tiempo viene dada por la ecuación

x=A·sen(ωt+φ)

Derivando con respecto al tiempo, obtenemos la velocidad del móvil

Derivando de nuevo respecto del tiempo, obtenemos la aceleración del móvil

Este resultado se suele expresar en forma de ecuación diferencial

Esta es la ecuación diferencial de un MAS donde x puede ser cualquier magnitud: un desplazamiento lineal, un desplazamiento angular, la carga de un condensador, una temperatura, etc.

Puede comprobarse que la solución de esta ecuación diferencial es

x=A sen(w t+j )

Condiciones iniciales

Conociendo la posición inicial x₀ y la velocidad inicial v₀ en el instante t=0.

x₀=A·senj
v₀=Aw·cosj

se determinan la amplitud A y la fase inicial φ

Dinámica de un M.A.S.

Aplicando la segunda ley de Newton obtenemos la expresión de la fuerza necesaria para que un móvil de masa m describa un M.A.S. Esta fuerza es proporcional al desplazamiento x y de sentido contrario a éste.

Como la  fuerza  F es conservativa. El trabajo de dicha fuerza es igual a la diferencia entre el valor inicial y el final de la energía potencial E_p.

La expresión de la energía potencial es

Donde c es cualquier constante. Se toma como nivel cero de la energía potencial E_p=0 cuando el móvil está en el origen, x=0, por lo que c=0

La energía total E, es la suma de la energía cinética E_k y de la energía potencial E_p que es constante.

Curva de energía potencial

La función E_p=mω²x²/2 representa una parábola cuyo vértice está en el origen, que tiene un mínimo en x=0 cuyo valor es E_p=0.

Las región donde se puede mover la partícula está determinada por la condición de que la energía cinética ha de ser mayor o igual a cero E_k>=0. En otras palabras, que la energía total sea mayor o igual que la energía potencial E>=E_p. Si la partícula tiene una energía total E, la partícula solamente se podrá mover en la región comprendida entre -A y +A, siendo A la amplitud de su M.A.S.

El módulo y el sentido de la fuerza vienen dados por la pendiente de la recta tangente cambiada de signo. Por tanto, la fuerza que actúa sobre la partícula es negativa a la derecha del origen y positiva a la izquierda.

En el origen la pendiente es nula, la fuerza es nula, una situación de equilibrio, que por coincidir con un mínimo de la energía potencial es de carácter estable.

ACTIVIDAD 1.- ELABORA UN MAPA CONCEPTUAL ACERCA DEL MAS Y ENVIALO

EJERCICIOS.- Lee con atención los ejercicios.

Ejercicio MAS-1         ¿Cuál es la constante de fase inicial j en la ecuación del movimiento x = A . sen (w t+j)? si las posiciones iniciales de la partícula son:  a) x = 0 b) x = -A c) x = +A d) x = A/2

Resolución: Para resolver este ejercicio debemos recurrir a la expresión que determina la posición x en un movimiento armónico simple .  la expresión como vimos es    por lo tanto la fase inicial se produce cuando t = 0 por lo que nos queda que  dado que el producto w t = 0  y en base a esta conclusión vamos a calcular cada uno de los valores solicitados               a)                   b)                c)                d)  Al no existir información complementaria, se optado por dar como respuesta, siempre el ángulo más pequeño que cumple la condición, dado que por ejemplo el caso a) podría tener respuesta pporque para ese valor también el seno del ángulo es 0. Respuesta:                     a) j = 0                 b) j = 3p/2                 c) j = p/2                 d) j = p/6

---

Ejercicio MAS-2   Una partícula tiene un desplazamiento x dado por la expresión en donde x viene expresada en metros y t en segundos. A) ¿Cuáles son la frecuencia y el período del movimiento? b) ¿Cuál es la mayor distancia que recorre la partícula desde su posición de equilibrio? c) ¿Dónde se encuentra la partícula en los instantes t = 0 y t = 0.5 s? d) ¿Cuál es la velocidad máxima que alcanza la partícula? e) Escribir la expresión de la v = f(t) f) Cuál es la aceleración máxima que alcanza la partícula? g) Escriba la expresión de la a = f(t)?

Resolución: Para resolver este ejercicio debemos conocer las expresiones de la posición , velocidad y aceleración de una partícula animada de un movimiento armónico simple, así como el concepto de frecuencia y período . Como vimos la expresión de la posición es  y comparándola con la expresión del desplazamiento de  tendremos que A = 3 m y w.t = 5pt por lo que el valor de w = 5p Como sabemos que existe una relación entre la frecuencia angular w y el período T o la frecuencia f obtendremos esos dos valores aplicando      y como       Por lo tanto la respuesta a la  pregunta a es período T = 0,4 s  y la frecuencia f = 2,5 Hz La respuesta a la  pregunta b surge sola, pues al obtener el valor de A, estamos obteniendo el máximo desplazamiento que tiene la partícula por lo que el máximo desplazamiento es de 3 m. Para responder a la pregunta c, debemos aplicar dos veces la expresión de x para los tiempo indicados 0 y 0,5 s. por lo tanto para t = 0 tendremos que x = 0 m    y    para t = 0,5 s tendremos que x = -3 m La pregunta d nos pide que calculemos la máxima velocidad que como vemos vale en valor absoluto A.w por lo que vmáx = 3 m . 5p rad/s = 15p m/s La pregunta e nos solicita que escribamos la expresión de la v = f(t) por lo que tendremos que como la expresión de v es La pregunta f nos solicita que calculemos la máxima aceleración que como vemos vale en valor absoluto A.w2 por lo que amáx = 3 m .(5p rad/s)2 =75 p2 rad/s2 . La pregunta g  nos solicita que escribamos la expresión de la a = f(t) por lo que tendremos que como la expresión de a es             Respuesta: a)  T = 0,4 s  f = 2,5 Hz b)  A = 3 m c)  x0s = 0 m  x0,5s = -3 m d)  vmáx = 15p m/s e)   f)   amáx = 75 p2 rad/s2  g)  a  = - 3.w2 . sen (5pt  + p)

Problemas (MAS)

ACTIVIDAD 2.-RESUELVE ESTOS PROBLEMAS y envialos incluyendo su desarrollo. 

1)   Si el movimiento de un pistón de un automóvil es aproximadamente armónico simple a) Si la carrera del pistón (2 veces la amplitud) es de 10 cm y la velocidad angular de 3600 rpm. Calcular la aceleración del pistón en el extremo de la carrera. b) Si el pistón tiene una masa de 500 g que fuerza se ejerce sobre él en ese punto, c) ¿Cuál es la velocidad del pistón en el punto medio de la carrera?

---

2)   Una masa de 2 kg cuelga de un resorte. Debido a ello se estira 10 cm. Si le provocamos posteriormente un estiramiento adicional de 5 cm de esa posición de equilibrio y se deja en libertad, calcule: a) La frecuencia angular b) La frecuencia c) la amplitud d) Escriba las expresiones de posición, velocidad y aceleración del movimiento

ELASTICIDAD

ELASTICIDAD

Mira la siguiente PPT 

Actividad 1.- Compara la información de la anterior PPT de Tippens con las siguientes slides de resumen, al final elabora un cuestionario de 15 preguntas abiertas y respuestas

PARTE II

Ley de Hooke (Elasticidad)

		Cuando un objeto de somete a fuerzas externas, sufre cambios de tamaño o de forma, o de ambos. Esos cambios dependen del arreglo de los átomos y su enlace en el material. Cuando un peso jala y estira a otro y cuando sele quita este peso y regresa a su tamaño normal decimos que es un cuerpo elástico. Elasticidad: Propiedad de cambiar de forma cuando actúa una fuerza de deformación sobre un objeto, y el objeto regresa a su forma original cuando cesa la deformación. Los materiales no deformables se les llama inhelásticos (arcilla,plastilina y masa de repostería). El plomo también es inhelástico, porque se deforma con facilidad de manera permanente. Si se estira o se comprime más allá de cierta cantidad, ya no regresa a su estado original, y permanece deformado, a esto se le llama límite elástico. *Cuando se tira o se estira de lago se dice que está en tensión (largas y delgadas). *Cuadno se aprieta o se comprime algo se dice que está en compresión (cortas y gruesas). Ley de Hooke: La cantidad de estiramiento o de compresión (cambio de longitud), es directamente proporcional a la fuerza aplicada. F=Kx PROBLEMA: *Para un resorte que cumple la ley de Hooke y que presenta como constante clásica de elasticidad el valor de 19.62 N/cm. Se le cuelga un objeto que causa una deformación de 58.86 cm. ¿Cuál es la masa del objeto? K=19.62 N/cm             F=kx                  m=Kx/g x=58.86                        W=mg         m=(19.62 N/cm)(58.86 cm)/9.81 g=9.81 m/s2                      Kx =mg             m/s2= 1154.83N/9.81 m/s2=                                                                                                    117.72 Kg m=117.72 Kg ACTIVIDAD 2.- Adjunta 5 problemas en donde utilices  la ley de Hooke  y la elasticidad.