El estudio del oscilador armónico constituye en Física un capítulo muy importante, ya que son muchos los sistemas físicos oscilantes que se dan en la naturaleza y que han sido producidos por el hombre.
Definición
Definición
Una partícula describe un Movimiento Armónico Simple (M.A.S.) cuando se mueve a lo largo del eje X, estando su posición x dada en función del tiempo t por la ecuación
x=A·sen(ωt+φ)
donde
- A es la amplitud.
- w la frecuencia angular.
- w t+j la fase.
- j la fase inicial.
Las características de un M.A.S. son:
- Como los valores máximo y mínimo de la función seno son +1 y -1, el movimiento se realiza en una región del eje X comprendida entre -A y +A.
- La función seno es periódica y se repite cada 2p, por tanto, el movimiento se repite cuando el argumento de la función seno se incrementa en 2p, es decir, cuando transcurre un tiempo P tal que w(t+P)+j=w t+j+2p .
P=2π/ω
Cinemática de un M.A.S.
En un movimiento rectilíneo, dada la posición de un móvil, obtenemos la velocidad derivando respecto del tiempo y luego, la aceleración derivando la expresión de la velocidad.
La posición del móvil que describe un M.A.S. en función del tiempo viene dada por la ecuación
x=A·sen(ωt+φ)
Derivando con respecto al tiempo, obtenemos la velocidad del móvil
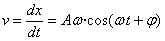
Derivando de nuevo respecto del tiempo, obtenemos la aceleración del móvil
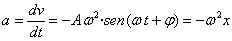
Este resultado se suele expresar en forma de ecuación diferencial
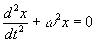
Esta es la ecuación diferencial de un MAS donde x puede ser cualquier magnitud: un desplazamiento lineal, un desplazamiento angular, la carga de un condensador, una temperatura, etc.
Puede comprobarse que la solución de esta ecuación diferencial es
x=A sen(w t+j )
Condiciones iniciales
Conociendo la posición inicial x0 y la velocidad inicial v0 en el instante t=0.
x0=A·senj
v0=Aw·cosj
v0=Aw·cosj
se determinan la amplitud A y la fase inicial φ
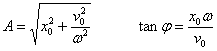
Dinámica de un M.A.S.
Aplicando la segunda ley de Newton obtenemos la expresión de la fuerza necesaria para que un móvil de masa m describa un M.A.S. Esta fuerza es proporcional al desplazamiento x y de sentido contrario a éste.
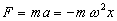
Como la fuerza F es conservativa. El trabajo de dicha fuerza es igual a la diferencia entre el valor inicial y el final de la energía potencial Ep.
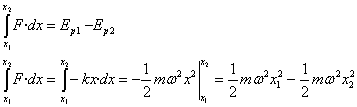
La expresión de la energía potencial es
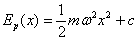
Donde c es cualquier constante. Se toma como nivel cero de la energía potencial Ep=0 cuando el móvil está en el origen, x=0, por lo que c=0
La energía total E, es la suma de la energía cinética Ek y de la energía potencial Ep que es constante.
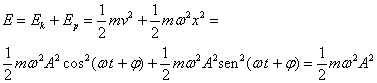
Curva de energía potencial
La función Ep=mω2x2/2 representa una parábola cuyo vértice está en el origen, que tiene un mínimo en x=0 cuyo valor es Ep=0.
Las región donde se puede mover la partícula está determinada por la condición de que la energía cinética ha de ser mayor o igual a cero Ek>=0. En otras palabras, que la energía total sea mayor o igual que la energía potencial E>=Ep. Si la partícula tiene una energía total E, la partícula solamente se podrá mover en la región comprendida entre -A y +A, siendo A la amplitud de su M.A.S.
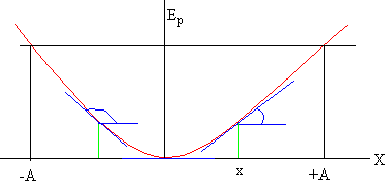
El módulo y el sentido de la fuerza vienen dados por la pendiente de la recta tangente cambiada de signo. Por tanto, la fuerza que actúa sobre la partícula es negativa a la derecha del origen y positiva a la izquierda.
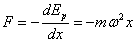
En el origen la pendiente es nula, la fuerza es nula, una situación de equilibrio, que por coincidir con un mínimo de la energía potencial es de carácter estable.
ACTIVIDAD 1.- ELABORA UN MAPA CONCEPTUAL ACERCA DEL MAS Y ENVIALO
EJERCICIOS.- Lee con atención los ejercicios.
Ejercicio MAS-1
¿Cuál es la constante de fase inicial j en la ecuación del movimiento x = A . sen (w t+j)? si las posiciones iniciales de la partícula son:
|
Resolución: Para resolver este ejercicio debemos recurrir a la expresión que determina la posición x en un movimiento armónico simple .
la expresión como vimos es
 por lo tanto la fase inicial se produce cuando t = 0 por lo que nos queda que  dado que el producto w t = 0
y en base a esta conclusión vamos a calcular cada uno de los valores solicitados
a)
b)
c)
d)
Al no existir información complementaria, se optado por dar como respuesta, siempre el ángulo más pequeño que cumple la condición, dado que por ejemplo el caso a) podría tener respuesta pporque para ese valor también el seno del ángulo es 0.
Respuesta:
a) j = 0
b) j = 3p/2
c) j = p/2
d) j = p/6
|
Ejercicio MAS-2
Una partícula tiene un desplazamiento x dado por la expresión
 en donde x viene expresada en metros y t en segundos. A) ¿Cuáles son la frecuencia y el período del movimiento? b) ¿Cuál es la mayor distancia que recorre la partícula desde su posición de equilibrio? c) ¿Dónde se encuentra la partícula en los instantes t = 0 y t = 0.5 s? d) ¿Cuál es la velocidad máxima que alcanza la partícula? e) Escribir la expresión de la v = f(t) f) Cuál es la aceleración máxima que alcanza la partícula? g) Escriba la expresión de la a = f(t)? |
Resolución: Para resolver este ejercicio debemos conocer las expresiones de la posición , velocidad y aceleración de una partícula animada de un movimiento armónico simple, así como el concepto de frecuencia y período .
Como vimos la expresión de la posición es
y comparándola con la expresión del desplazamiento de tendremos que A = 3 m y w.t = 5pt por lo que el valor de w = 5p
Como sabemos que existe una relación entre la frecuencia angular w y el período T o la frecuencia f obtendremos esos dos valores aplicando
 y como 
Por lo tanto la respuesta a la pregunta a es período T = 0,4 s y la frecuencia f = 2,5 Hz
La respuesta a la pregunta b surge sola, pues al obtener el valor de A, estamos obteniendo el máximo desplazamiento que tiene la partícula por lo que el máximo desplazamiento es de 3 m.
Para responder a la pregunta c, debemos aplicar dos veces la expresión de x para los tiempo indicados 0 y 0,5 s.
 
por lo tanto para t = 0 tendremos que x = 0 m y para t = 0,5 s tendremos que x = -3 m
La pregunta d nos pide que calculemos la máxima velocidad que como vemos vale en valor absoluto A.w por lo que vmáx = 3 m . 5p rad/s = 15p m/s
La pregunta e nos solicita que escribamos la expresión de la v = f(t) por lo que tendremos que como la expresión de v es
La pregunta f nos solicita que calculemos la máxima aceleración que como vemos vale en valor absoluto A.w2 por lo que amáx = 3 m .(5p rad/s)2 =75 p2 rad/s2 .
La pregunta g nos solicita que escribamos la expresión de la a = f(t) por lo que tendremos que como la expresión de a es
Respuesta:
|
Problemas (MAS)
ACTIVIDAD 2.-RESUELVE ESTOS PROBLEMAS y envialos incluyendo su desarrollo.
1) Si el movimiento de un pistón de un automóvil es aproximadamente armónico simple a) Si la carrera del pistón (2 veces la amplitud) es de 10 cm y la velocidad angular de 3600 rpm. Calcular la aceleración del pistón en el extremo de la carrera. b) Si el pistón tiene una masa de 500 g que fuerza se ejerce sobre él en ese punto, c) ¿Cuál es la velocidad del pistón en el punto medio de la carrera?
|
2) Una masa de 2 kg cuelga de un resorte. Debido a ello se estira 10 cm. Si le provocamos posteriormente un estiramiento adicional de 5 cm de esa posición de equilibrio y se deja en libertad, calcule:
a) La frecuencia angular
b) La frecuencia
c) la amplitud
d) Escriba las expresiones de posición, velocidad y aceleración del movimiento
|
No hay comentarios:
Publicar un comentario