EQUILIBRIO ROTACIONAL. MOVIMIENTO DE TORSIÓN (TORQUE)
RESUMEN
Cuando sobre un cuerpo actúan fuerzas que no tienen la misma línea de acción o no se intersectan en un punto común, puede haber rotación. En este capítulo se ha presentado el concepto de momento de torsión como una medida de la tendencia a girar. Los principales conceptos se resumen a continuación:
- El brazo de palanca de una fuerza es la distancia perpendicular que hay entre la línea de acción de la fuerza y el eje de rotación.
- Línea de acción es la proyección de la fuerza, en cualquier sentido (hacia delante o hacia atrás.
- El momento de torsión con respecto a un eje determinado, se define como el producto de la magnitud de una fuerza por su brazo de palanca:
Momento de = fuerza x brazo de palanca Torsión
τ = F x b
Es positivo si tiende a producir movimiento en sentido contrario al avance de las agujas del reloj sentido (+) y negativo si el movimiento se produce en el mismo sentido de las agujas (sentido (-)
- El momento de torsión resultante τR con respecto a un eje particular A es la suma algebraica de los momentos de torsión producidos por cada fuerza. Los signos se determinan por la convención ya mencionada.
τR = ± F1 · b1 ± F2 · b2 ± F3 · b3 ± F4 · b4 ± …………..
- Equilibrio rotacional: Un cuerpo en equilibrio rotacional no tiene un momento de torsión resultante que actúe sobre él. En tales casos, la suma de todos los momentos de torsión respecto a cualquier eje debe ser igual a cero.
τR = 0
Los ejes pueden elegirse en cualquier parte puesto que el sistema no tiene tendencia a girar respecto a cualquier punto. Ésta se llama segunda condición de equilibrio y puede escribirse como: Σ τ = 0 La suma de todos los momentos de torsión respecto a cualquier punto es cero.
- El equilibrio total existe cuando se satisfacen la primera y la segunda condiciones de equilibrio. En tales casos, se pueden escribir tres ecuaciones independientes:
Σ Fx = 0 ; Σ Fy = 0 ; Σ τ = 0
Escribiendo estas tres ecuaciones para una situación específica se pueden determinar fuerzas, distancias y momentos de torsión desconocidos.
- El centro de gravedad de un cuerpo es el punto a través del cual actúa el peso resultante, independientemente de cómo esté orientado el cuerpo. Para las aplicaciones que incluyen momentos de torsión, se puede considerar que el peso total del objeto actúa en este punto.
EJERCICIOS
1.- Dada la siguiente figura,¿Cuál es el momento de torsión producido en la tuerca?
2.- Un puntal uniforme de 200 Ib de peso y 24 ft de longitud está sostenido por un cable, como se muestra en la figura 4-9. El puntal se apoya en la pared y el cable forma un ángulo de 30° con respecto al puntal, que está en posición horizontal. Si se cuelga del extremo derecho una carga de 500 Ib, ¿cuál es la tensión T del cable? ¿Cuáles son las componentes horizontal y vertical de la fuerza ejercida por el pivote?
3.- Una escalera de 5 m de longitud se apoya contra una pared vertical sin rozamiento, con su extremo inferior a 3 m de la pared. La escalera pesa 80 Newton y su centro de gravedad está en su punto medio. El coeficiente estático de rozamiento entre el pie de la escalera y el suelo es 0,4
- ¿A qué altura puede subir sobre la escalera un hombre que pesa 90 Newton, sin que esta comience a deslizar?
- ¿Cuánto puede separarse el pie de la pared, sin que comience a deslizar, cuando no actúa ninguna carga sobre ella salvo su propio peso?
4.- Una viga de 150 N y 12 m de largo es transportada por tres hombres. Uno colocado en un extremo y los otros dos soportando una barra transversal. ¿Cuál debe ser la posición de la barra transversal para que los 3 hombres soporten el mismo peso?
5.- Una escalera AB descansa contra una pared vertical BO ( sin fricción ) formando un ángulo de 60º con el suelo. La escalera pesa 200 N ; determinar las fuerzas que ejercen la pared y el suelo.
6.- Una viga horizontal uniforme de 8 m de largo y 200 N de peso está unida a un muro por medio de una conexión de pasador. Su extremo alejado está sostenido por un cable que forma un ángulo de 53º con la horizontal. Si una persona de 600 N está parada a 2 m del muro, encuentre la tensión en el cable y la fuerza ejercida por el muro sobre la viga.
7.- Determine la tensión en el cable de la figura, si el puntal tiene un peso de 300 N
8.- a) Encuentre el momento de torsión resultante respecto al punto A de la figura.
- Encuentre el momento de torsión resultante respecto al punto B de la figura.
RESPUESTAS
3A .-2.8 M
3B.- 3.1 M
4.- 3 M A LA IZQUIERDA DEL PESO
6.-R: T = 313 N; F = 581 N; 71º
7.-
8.-
TEMA 2
MOVIMIENTO UNIFORMEMENTE ACELERADO
M u a from votrefolie
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
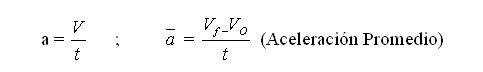
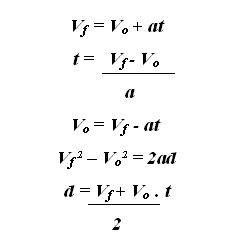








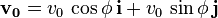

 e
e es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal. es la aceleración de la gravedad.
es la aceleración de la gravedad.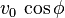 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.
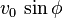 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial.
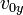

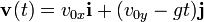




No hay comentarios:
Publicar un comentario