FACTORIZACION

DA CLICK EN EL SIGUIENTE ENLACE  AQUI  Revisa este apunte para refrescar tus conocimientos sobre la factorización.

INTRODUCCIÓN

Para entender la operación algebraica llamada factorización es preciso repasar los siguientes conceptos:

A.-Cualquier expresión que incluya la relación de igualdad (=) se llama ecuación.

B.-Una ecuación se denomina identidad si la igualdad se cumple para cualquier valor de las variables; si la ecuación se cumple para ciertos valores de las variables pero no para otros, la ecuación es condicional.

C.-Un término es una expresión algebraica que sólo contiene productos de constantes y variables; 2x, – a, 3x son algunos ejemplos de términos.

D.-La parte numérica de un término se denomina coeficiente.

E.-Los coeficientes de cada uno de los ejemplos anteriores son 2, – 1, y 3.

F.-Una expresión que contiene un solo término se denomina monomio; si contiene dos términos se llama binomio y si contiene tres términos, es un trinomio.

G.-Un polinomio es una suma (o diferencia) finita de términos.

En este contexto, el grado es el mayor exponente de las variables en un polinomio. Por ejemplo, si el mayor exponente de la variable es 3, como en ax³ + bx² + cx, el polinomio es de tercer grado.

H.-Una ecuación lineal en una variable es una ecuación polinómica de primer grado; es decir, una ecuación de la forma ax + b = 0.

I.-Se les llama ecuaciones lineales porque representan la fórmula de una línea recta en la geometría analítica.

J.-Una ecuación cuadrática en una variable es una ecuación polinómica de segundo grado, es decir, de la forma ax² + bx + c = 0.

K.-Un número primo es un entero (número natural) que sólo se puede dividir exactamente por sí mismo y por 1. Así, 2, 3, 5, 7, 11 y 13 son todos números primos.

L.-Las potencias de un número se obtienen mediante sucesivas multiplicaciones del número por sí mismo. El término a elevado a la tercera potencia, por ejemplo, se puede expresar como a·a·a o a³

M.-Los factores primos de un cierto número son aquellos factores en los que éste se puede descomponer de manera que el número se puede expresar sólo como el producto de números primos y sus potencias.

Descomposición de números naturales en sus factores primos

Por ejemplo, un número natural como 20 puede expresarse como un producto de números de diferentes formas:

20 = 2 • 10 = 1 • 20 = 4 • 5

En cada uno de estos casos, los números que forman el producto son los factores.

Es decir, cuando expresamos el número 20 como el producto 2 • 10, a cada uno de los números (2 y 10) se les denomina factor.

En el caso de 1 • 20 los factores son 1 y 20 y finalmente en el caso de 4 • 5, los factores son 4 y 5.

Cada uno de los números 1, 2, 4, 5, 10, 20 se denominan a su vez divisores de 20.

Otro ejemplo, los factores primos de 15 son 3 y 5. Del mismo modo, como 60 = 2² • 3 • 5, los factores primos de 60 son 2, 3 y 5.

Debe recordarse, además, que cuando un número es divisible únicamente por sí mismo y por la unidad el número se denominaprimo.

Factorización y productos notables

1.-Así como los números naturales pueden ser expresados como producto de dos o más números, los polinomios pueden ser expresadas como el producto de dos o más factores algebraicos.

2.-Cuando un polinomio no se puede factorizar se denomina irreducible. En los casos en que la expresión es irreducible, solo puede expresarse como el producto del número 1 por la expresión original.

3.-Al proceso de expresar un polinomio como un producto de factores se le denomina factorización.

4.-El proceso de factorización puede considerarse como inverso al proceso de multiplicar.

Factorizar, entonces, quiere decir identificar los factores comunes a todos los términos y agruparlos.

5.-Los factores comunes son aquellos números que aparecen multiplicando a todos los términos de una expresión algebraica.

Estos números pueden estar dados explícitamente o representados por letras.

Así, factorizar un polinomio es descomponerlo en dos o más polinomios llamados factores, de tal modo que al multiplicarlos entre sí se obtenga el polinomio original.

En otras palabras, dada una expresión algebraica complicada, resulta útil, por lo general, el descomponerla en un producto de varios términos más sencillos.

Por ejemplo, 2x³ + 8x²y se puede factorizar, o reescribir, como 2x²(x + 4y).

Algunos ejemplos:

De la expresión    ab² + 3cb - b³ podemos factorizar  b

y obtenemos la expresión:   b(ab + 3c - b²) (1)

Veamos paso a paso cómo se obtuvo la expresión:

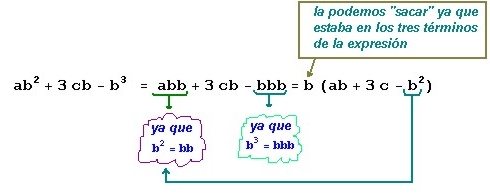
ahora podríamos reacomodar la expresión que queda dentro del paréntesis:

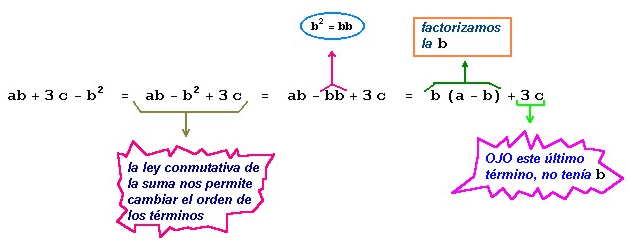
Finalmente si sustituimos este último resultado en (1), obtenemos:

ab² + 3cb - b³ = b (b (a - b) + 3c)

ab² + 3cb - b³ = b (ab - b² + 3c)

ab² + 3cb - b³ = b (ab +3c –b²)

6.-Por otro lado, algunos productos sencillos que tienen una estructura determinada y que pueden ser evaluados de forma directa se denominan Productos notables.

En general los casos de factorización corresponden a los casos de productos notables.

Antes de mostrar ejercicios de aplicación de factorización y productos notables, es necesario recordar la forma de hallar el máximo común divisor (mcd) de un conjunto de números dados.

Ejemplo: Determinar el máximo común divisor (mcd) de los números 56, 42 y 28.

El máximo común divisor de un conjunto de números dados corresponde al mayor número natural que los divide simultáneamente, con residuo cero.

Para hallar el mcd de un conjunto determinado de números, estos se dividen simultáneamente por los diferentes números primos (tomados en orden ascendente, y desechando los números primos por los cuales no se pueda hacer la división con residuo cero detodos los números de la fila) según el arreglo mostrado a continuación.

El proceso termina, cuando los números que aparecen en la fila inmediatamente inferior a la última división simultánea, no pueden dividirse simultáneamente por algún número primo.

El mcd buscado es el producto de los números primos que aparecen a la derecha:

56	42	28	÷	2
28	21	14	÷	7
4	3	2

Los números originales (56, 42, 28) se escriben desde la izquierda hacia la derecha.

A la derecha de ellos se escribe el 2 (primer número primo de la lista) y se divide cada uno de estos números por 2, escribiendo el resultado obtenido en la misma columna del número original.

La segunda fila muestra estos resultados.

Como los números 28, 21 y 14 no pueden dividirse simultáneamente por 3, este número primo se desecha.

De forma similar se desecha el 5.

El siguiente número primo en la lista es 7.

En este caso se puede hacer la división simultáneamente obteniéndose los números 4, 3 y 2.

Esta última fila no puede dividirse simultáneamente ni por 2 ni por 3.

Como el siguiente número primo (5) es mayor que 4, el proceso termina.

Por lo tanto, el mcd de los números 56, 42 y 28 es el producto de los números primos de la derecha: 2 • 7 = 14

Lo anterior se expresa como: mcd (56, 42, 28) = 14  (el máximo común divisor de los números 56, 42 y 28 es igual a 14)

Ejemplo: Factorizar  9x + 6y - 12z

Este es un ejemplo sencillo de la factorización por factor común.

Dada una expresión algebraica se encuentra el máximo común divisor (mcd) de los coeficientes de los términos de la expresión algebraica.

Este mcd corresponde al coeficiente del factor común.

Para la parte literal se toman las variables comunes a todos los términos con el menor exponente que aparezca.

Para este ejercicio el mcd de 9, 6 y 12 es 3; además como no hay variables comunes en los tres términos tenemos:

9x + 6y - 12z = 3(3x + 2y - 4z)

es decir 9x  + 6y - 12z se ha expresado como el producto de los factores 3 y 3x + 2y - 4z.

Ejemplo: Factorizar  9xy² + 6y⁴ - 12 y³z

En este caso además del factor común 3 (mcd de 9, 6, 12) la variable y es común a los tres términos. La menor potencia común es  y²por lo tanto la factorización queda:

9xy² + 6y⁴ - 12y³z = 3y²(3x + 2y² - 4yz)

Los factores en este caso son 3x + 2y² - 4yz  y  3y². Para verificar, al realizar el producto indicado se obtiene la expresión original:

3y²(3x + 2y² - 4yz) = (3y² * 3x) + (3y² * 2y²) - (3y² * 4yz)

= 9xy² + 6y⁴ - 12y³z

Nótese que se ha aplicado la propiedad distributiva del producto. En general no es necesario hacer la verificación de la factorización, pero es conveniente cuando existan dudas sobre el resultado obtenido

FACTORIZACIÓN DE POLINOMIOS

Para factorizar polinomios hay varios métodos:

1. Sacar factor común: Es aplicar la propiedad distributiva de la multiplicación respecto de la suma, Así, la propiedad distributiva dice:

Pues bien, si nos piden factorizar la expresión , basta aplicar la propiedad distributiva y decir que

Cuando nos piden sacar factor común o simplemente factorizar y hay coeficientes con factores comunes, se saca el máximo común divisor de dichos coeficientes. Por ejemplo, si nos piden factorizar la expresión , será

donde 6 es el máximo común divisor de 36, 12 y 18

Para comprobar si la factorización se ha hecho correctamente, basta efectuar la multiplicación, aplicando la propiedad distributiva de la parte derecha de la igualdad, y nos tiene que dar la parte izquierda.

Otro ejemplo: Factorizar 

 ¡Atención a cuando sacamos un sumando completo!, dentro del paréntesis hay que poner un uno. Tener en cuenta que si hubiéramos puesto  y quiero comprobar si está bien, multiplico y me da  pero no  como me tendría que haber dado.

Sin embargo si efectúo 

Otros ejemplos:

2. Si se trata de una diferencia de cuadrados: Es igual a suma por diferencia.

Se basa en la siguiente fórmula

Pero aplicada al revés, o sea que si me dicen que factorice  escribo

Otros ejemplos de factorización por este método:

3. Si se trata de un trinomio cuadrado perfecto: Es igual al cuadrado de un binomio

Se basa en las siguientes fórmulas

   y    

Así si nos dicen que factoricemos: , basta aplicar la fórmula anterior y escribir que

Otros ejemplos de factorización por este método:

1. Si se trata de un trinomio de segundo grado: O sea un polinomio de este tipo

, siendo a, b y c números

Se iguala el trinomio a cero , se resuelve la ecuación , y si tiene dos soluciones distintas,  y se aplica la siguiente fórmula: 

Veamos un ejemplo: Factorizar el polinomio 

Igualamos a cero 

Resolvemos la ecuación , y separando las dos soluciones , , y aplicando la fórmula, teniendo en cuenta que a=2

2. Para cualquier polinomio que tenga raíces enteras se puede aplicar la regla de Ruffini: Decir que un polinomio tienes raíces enteras es encontrar valores de x números enteros que al sustituirlos en el polinomio nos da cero.

Si un polinomio de , por ejemplo, cuarto grado  tiene cuatro raíces enteras, , ,  y  se factoriza así:

Pero ¿cómo se obtienen las raíces?, por la regla de Ruffini

Ejemplo: Factorizar 

Se aplica la regla de Ruffini, probando los divisores del término independiente, en este caso de 12. O sea que se prueba con 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 12 y –12

Probemos con uno

Se copian los coeficientes del polinomio:

1

-4

-1

16

-12

Y se escribe en una segunda línea el número uno

	1	-4	-1	16	-12
1

El primer coeficiente se copia abajo en una tercera línea

	1	-4	-1	16	-12
1
	1

Se multiplica ese coeficiente, uno (1), por el número que estamos probando, en este caso también uno (1), o sea uno por uno = uno (1). Este uno se escribe debajo del siguiente coeficiente, o sea del –4

	1	-4	-1	16	-12
1		1
	1

Se suma –4+1=-3

	1	-4	-1	16	-12
1		1
	1	-3

Se multiplica –3 por 1=-3 y se escribe debajo del siguiente coeficiente, -1

	1	-4	-1	16	-12
1		1	-3
	1	-3

Se suma –3-1=-4 y así sucesivamente

	1	-4	-1	16	-12
1		1	-3	-4	12
	1	-3	-4	12	0

Como vemos la última suma ha dado cero. Eso quiere decir que uno es una raíz del polinomio y que nos sirve para factorizar.

Si hubiera dado distinto de cero habría que seguir probando los demás divisores de 12.

Los coeficientes que han quedado en la última fila, en realidad son los coeficientes del cociente de dividir el polinomio entre x-1, y la última suma es el resto de dicha división.

Si escribimos la relación fundamental de una división entera, o sea que

Dividendo=Divisor x Cociente+Resto

==

De hecho ya hemos factorizado el polinomio, pero el segundo factor de tercer grado hay que intentar seguir factorizando, de nuevo por la regla de Ruffini.

Aplicando sucesivas veces esta regla queda:

	1	-4	-1	16	-12
1		1	-3	-4	12
	1	-3	-4	12	0
2		2	-2	-12
	1	-1	-6	0
-2		-2	6
	1	-3	0

Como las raíces son, 1, 2 y –2 y el último cociente es x-3

La factorización final es:

= 

Si en las sucesivas pruebas no encontramos ningún resto cero, quiere decir que el polinomio no se puede factorizar dentro de los números reales.

EN RESUMEN

Muchas veces se pueden combinar estos cinco métodos. Según como sea el polinomio hay métodos que se pueden aplicar y otros que no. Se aconseja que se intenten aplicar los cinco métodos sucesivamente, sobre todo, si se puede sacar factor común se hace en primer lugar, y si luego en uno de los factores se puede seguir aplicando otros de los métodos, se aplica.

EJEMPLOS: Factorizar los siguientes polinomios

1.- 

Podemos aplicar el primer método, o sea sacar factor común

El segundo factor, o sea el paréntesis, es un trinomio de segundo grado y cuadrado perfecto. Se puede factorizar por el tercero, cuarto o quinto método. Apliquemos el tercero y queda:

=

2.- 

Primero sacamos factor común: 

Al paréntesis le podemos aplicar el segundo método y queda: = 

Y aún más, al segundo paréntesis le podemos volver a aplicar el segundo método:

=

El polinomio de segundo grado que queda en el tercer paréntesis no se puede factorizar. Si probamos el cuarto método, igualando a cero y resolviendo la ecuación queda 

 que no tiene solución real.

3.- 

Sólo podemos aplicar el quinto método, o sea Ruffini:

	1	-12	41	-30
1		1	-11	30
	1	-11	30	0
5		5	-30
	1	-6	0

=

4.- 

Primero sacamos factor común

=

Igualamos a cero el paréntesis y resolvemos la ecuación:  que origina dos soluciones, -3 y –2, por tanto la factorización completa es:

=

DA CLICK EN LOS SIGUIENTES ENLACES

A.-EJEMPLOS Y TIPOS DE FACTORIZACION

B.- EJERCICIOS RESUELTOS DEL LIBRO DE BALDOR

EJERCICIOS PARA RESOLVER

EJERCICION 89.
BALDOR
14x ²y ²-28x ³+56x4=14x ²(y ²-2x+4x ²)

34ax ²+51a ²y-68ay ²=17a(2x ²+3ay-4y ²)

96-48mn ²+144n ³=48(2-mn ²+3n ³)

a ²b ²c ²-a ²c ²x ²+a ²c ²y ²=a ²c ²(b ²-x ²+y ²)

55m ²n ³x+110m ²n ³x ²-220m ²y ³=55m ²(n ³x+2n ³x ²-4y ³)
DESCOMPOSICION EN DOS FACTORES:

(a+b-c)(x-3)-(b-c-a)(x-3)=

=(x-3) [ (a+b-c)-(b-c-a)] =(x-3)(a+b-c-b+c+a)

=(x-3)2a
3x(x-1)-2y(x-1)+z(x-1)=

=(x-1)(3x-2y+z)

a(n+1) -b(n+1)-n-1=

=a(n+1)-b(n+1)-1(n+1)=

=(n+1)(a-b-1)
X(a+2)-a-2+3(a+2)=

=x(a+2)-1(a+2)+3(a+2)=

(a+2)(x+2)

X(a+2)-a-2+3(a+2)=

=x(a+2)-1(a+2)+3(a+2)=

(a+2)(x+2)

(1+3a)(x+1)-2a(x+1)+3(x+1)=

=(x+1)(1+3a-2a+3)=

=(x+1)(a+4)
(3x+2)(x+y-z)-(3x+2)-(x+y-1)(3x+2)=

=(3x+2) [ (x+y-z)(-1)-(x+y-1) ]
=(3x+2)(-z)