Un polinomio es una expresión algebraica de la forma:

P(x) = a_n xⁿ + a_{n - 1} x^{n - 1} + a_{n - 2} x^{n - 2} + ... + a₁ x¹ + a₀

Siendo a_n, a_{n -1} ... a₁ , a_o números, llamados coeficientes.

n un número natural.

x la variable o indeterminada.

a_n es el coeficiente principal.

a_o es el término independiente.

Grado de un polinomio

El grado de un polinomio P(x) es el mayor exponente al que se encuentra elevada la variable x.

Clasificación de un polinomio según su grado

Primer grado

P(x) = 3x + 2

Segundo grado

P(x) = 2x² + 3x + 2

Tercer grado

P(x) = x³ − 2x²+ 3x + 2

Tipos de polinomios

Polinomio nulo

Es aquel polinomio que tiene todos sus coeficientes nulos.

Polinomio homogéneo

Es aquel polinomio en el todos sus términos o monomios son del mismo grado.

P(x) = 2x² + 3xy

Polinomio heterogéneo

Es aquel polinomio en el que sus términos no son del miso grado.

P(x) = 2x³ + 3x² - 3

Polinomio completo

Es aquel polinomio que tiene todos los términos desde el término independiente hasta el término de mayor grado.

P(x) = 2x³ + 3x² + 5x - 3

Polinomio ordenado

Un polinomio está ordenado si los monomios que lo forman están escritos de mayor a menor grado.

P(x) = 2x³ + 5x - 3

Polinomios iguales

Dos polinomios son iguales si verifican:

1Los dos polinomios tienen el mismo grado.

2Los coeficientes de los términos del mismo grado son iguales.

P(x) = 2x³ + 5x − 3

Q(x) = 5x − 3 + 2x³

Polinomios semejantes

Dos polinomios son semejantes si verifican que tienen la misma parte literal.

P(x) = 2x³ + 5x − 3

Q(x) = 5x³ − 2x − 7

Valor numérico de un polinomio

Es el resultado que obtenemos al sustituir la variable x por un número cualquiera.

P(x) = 2x³ + 5x − 3 ; x = 1

P(1) = 2 · 1³ + 5 · 1 − 3 = 2 + 5 - 3 = 4

Polinomios Suma Resta Producto Cociente Regla de Ruffini Teorema del resto Factorización de polinomios

Suma

Suma de polinomios.Para sumar polinomios, sumamos entre sí aquellos monomios que tengan la misma parte literal. 

Por ejemplo, consideremos los polinomios
P(x)= 3x⁵ + 2x³ - 5x² + 6 y Q(x) = 8x³ + 3x² - x - 4
El polinomio resultante de la suma P(x) + Q(x)= 3x⁵ + 10x³ - 2x² - x + 2
Fíjate, aquellos monomios cuya parte literal aparece en un polinomio los hemos copiado y hemos sumado aquellos monomios que tenían la misma parte literal:
2x³ + 8x³ = 10x³
-5x² + 3x² = -2x³
6 - 4 = 2

Resta

Resta de polinomios.Para restar polinomios, restamos entre sí aquellos monomios que tengan la misma parte literal.

Por ejemplo, consideremos los polinomios
P(x)= 3x⁵ + 2x³ - 5x² + 6 y Q(x) = 8x³ + 3x² - x - 4
El polinomio resultante de la resta P(x) - Q(x)= 3x⁵ - 6 x³ - 8x² + x + 10
Fíjate, aquellos monomios cuya parte literal aparece sólo en P(x) se dejan tal cual, a los que aparecen sólo en Q(x) se les cambia el signo y restamos aquellos monomios que tenían la misma parte literal:
2x³ - 8x³ = -6x³
-5x² - 3x² = -8x³
6 - (-4) = 10

Solución:   x5 x4 x3 x2 x

Producto

Producto de polinomios.
Para multiplicar dos polinomios multiplicamos cada monomio del primer polinomio por cada polinomio del segundo. Luego sumamos aquellos monomios con la misma parte literal.

Solución: x6 x5 x4 x3 x2 x

Cociente

Solución: Cociente:     x3 x2 x Resto:

Regla de Ruffini

La regla de Ruffini es un algoritmo que permite obtener fácilmente el cociente y el resto de la división de un polinomio por un binomio de la forma x-a. Veamos el algoritmo con un ejemplo, consideremos P(x)=2x³ + x² - 3x + 5 y Q(x)=x-1. La división se realiza como sigue:

1.Se ordena el polinomio P(x) de mayor a menor grado y se colocan los coeficientes de cada término . Si no apareciese algún término entre el de mayor grado y el de menor se coloca un 0. A la izquierda se pone el número que se resta a x en Q(x), en nuestro caso 1 y se baja el coeficiente del término de mayor grado, este paso se corresponde con la figura 1.

2. Se multiplica el coeficiente que se ha bajado (2) por el que se ha colocado a la izquierda (1). El resultado del producto se coloca debajo del coeficiente del término siguiente y se suman. Figura 2

3. El resultado de la suma se vuelve a multiplicar por el número situado a la izquierda y se repite el proceso. Figuras 3 y 4.

4. El último número (recuadro rojo en Fig. 4) se corresponde con el resto de la división mientras que el resto de números de la fila inferior son los coeficientes del cociente.
Resto = 5 y C(x)=2x² + 3x por tanto 2x³ + x² - 3x + 5 =(x-1) (2x² + 3x) +5

Usando la regla de Ruffini, divide el polinomio entre Q(x)=

Solución:

Cociente:

x3

x2

x

Resto:

Teorema del resto

Evaluar un polinomio
Evaluar un polinomio consiste en determinar qué valor toma el polinomio cuando la indeterminada (x) se sustituye por un número.

Consideramos el polinomio P(x)=2x³-5x+3 evaluar el polinomio en 1 consiste en sustituir la indeterminada por 1 (x=1) quedando P(1)=2·1³-5·1+3=2-5+3=0.

Teorema del resto
El valor que se obtiene al evaluar un polinomio en x=a coincide con el resto de dividir ese polinomio por x-a.
Si dividimos un polinomio P(x) por x-a se obtendrá un cociente C(x) y un resto r.
En toda división el dividendo P(x) es igual al divisor x-a por el cociente C(x) más el resto r , es decir, P(x)=(x-a)·C(x) + r.
Al evaluar el polinomio en el punto se tiene
P(a)=(a-a)·C(a) + r , como a-a =0 entonces P(a) = r
Gracias a este teorema podemos usar la regla de Ruffini para evaluar un polinomio en un punto.

Evalúa el polinomio P(x)=2x³-5x+3 en x=1 usando la regla de Ruffini

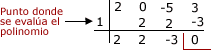
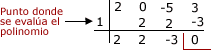
P(1) = 0 ya que 0 es el resto de la división de P(x) entre x-a

Usando la regla de Ruffini, evalúa el polinomio  en 

Solución:

Factorización de un polinomio

Raíz de un polinomio 
Diremos que un número x=a es raíz de un polinomio P(x) si al evaluar P en a se anula, es decir, P(a)=0 .
Un polinomio es divisible por otro si al realizar la división el resto es 0.
Por tanto, si a es raíz de un polinomio P(x), teniendo en cuenta el teorema del resto, podemos afirmar que P(x) es divisible por x-a.

Si a es una raíz de un polinomio entonces a divide al término independiente.
Dado P(x) = c_nxⁿ + c_n-1x^n-1 +...+ c₁x + c₀ y sea a una raíz de P
P(a) = c_naⁿ + c_n-1a^n-1 +...+ c₁a + c₀ , al sea a una raíz, P(a) = 0
c_naⁿ + c_n-1a^n-1 +...+ c₁a + c₀ = 0 pasamos el término independiente al segundo miembro y sacamos factor común a a, queda a·( c_na^n-1 + c_n-1a^n-2 +...+ c₁ ) = - c₀de aquí se deduce que la raíz es divisor del término independiente.

Esto nos permite buscar las raíces entre los divisores del término independiente

Factorizar un polinomio
Factorizar consiste en descomponer un polinomio como producto de otros más simples. Cuando un polinomio no se puede poner como producto de otros más simples se dice que es irreducible.
Para factorizar un polinomio hallamos su raíces, si a es una raíz de P(x), entoncesP(x)=(x-a)·P₁(x), así hemos descompuesto P como producto de dos polinomios, reiteramos el proceso, ahora con P₁y seguimos hasta que nos encontremos con un polinomio irreducible.

Factoriza el polinomio P(x)=2x⁵ -3x³ +4x² -9x + 6
Usamos la regla de Ruffini, los candidatos a raíz serán los divisores de 6, es decir, 1, -1, 2, -1, 3, -2, 6, -6.
Vamos probando hasta que encontremos un valor cuyo resto es 0, repetimos el proceso con los coeficientes del polinomio cociente hasta que no podamos continuar, porque lleguemos a un polinomio irreducible.
En el ejemplo hemos llegado a un momento en el que no hemos encontrado raíces enteras 2x² +3, con este polinomio podemos continuar planteando una ecuación de segundo grado, aún así no tiene raíces reales por tanto es irreducible. En la figura de la derecha se observa el proceso.
La factorización queda: 
2x⁵ -3x³ +4x² -9x + 6 =(x-1)²(x+2)(2x² +3)

Usando el método de Rufini halla las raíces del siguiente polinomio:
        

Raíces a=  b=  c=  d= 

RESUMEN

Polinomios

Un polinomio es así: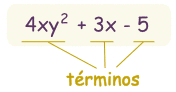

un ejemplo de polinomio este tiene 3 términos

Están hechos de:

	constantes (como 3, -20, o ½)
	variables (como x e y)
	exponentes (como el 2 en y2) pero sólo pueden ser 0, 1, 2, 3, ... etc

Que se pueden combinar usando:

+ - ×	sumas, restas y multiplicaciones...
	... ¡pero no divisiones!

Estas reglas hacen que los polinomios sean simples, ¡así es fácil trabajar con ellos!

¿Son polinomios o no?

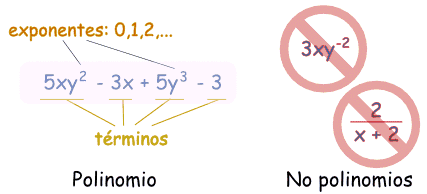
Estos son polinomios:

• 3x
• x - 2
• 3xyz + 3xy²z - 0.1xz - 200y + 0.5

Y estos no son polinomios

• 2/(x+2) no lo es, porque dividir no está permitido
• 3xy^-2 no lo es, porque un exponente es "-2" (los exponentes sólo pueden ser 0,1,2,...)

Pero esto sí está permitido:

• x/2 está permitido, porque también es (½)x (la constante es ½, o 0.5)
• también 3x/8 por la misma razón (la constante es 3/8, o 0.375)

Monomios, binomios, trinomios

Hay nombres especiales para los polinomios con 1, 2 o 3 términos:

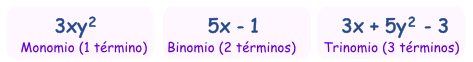
¿Cómo te aprendes los nombres? ¡Piensa en bicicletas!

(También existen cuatrinomio (4 términos) y quintinomio (5 términos), pero se usan poco)

Muchos términos

Los polinomios pueden tener montones de términos, pero no infinitos términos.

¿Qué tienen de especial los polinomios?

Por su definición tan estricta, es fácil trabajar con polinomios.

Por ejemplo sabemos que:

• Si sumas o restas polinomios te sale un polinomio
• Si multiplicas polinomios te sale un polinomio

Así que puedes hacer muchas sumas y multiplicaciones con ellos, y siempre sale un polinomio al final.

Grado

El grado de un polinomio con una sola variable es el mayor exponente de esa variable.

Ejemplo:

El grado es 3 (el mayor exponente de x) EJERCICIOS PARA RESOLVER Ejercicios y problemas de polinomios 1 Di si las siguientes expresiones algebraicas son polinomios o no. En caso afirmativo, señala cuál es su grado y término independiente. 1x4 − 3x5 + 2x2 + 5 2  + 7X2 + 2 31 − x4 4 5x3 + x5 + x2 6x − 2x−3 + 8 7 2Escribe: 1Un polinomio ordenado sin término independiente. 2Un polinomio no ordenado y completo. 3Un polinomio completo sin término independiente. 4Un polinomio de grado 4, completo y con coeficientes impares. 3Dados los polinomios: P(x) = 4x2 − 1 Q(x) = x3 − 3x2 + 6x − 2 R(x) = 6x2 + x + 1 S(x) = 1/2x2 + 4 T(x) = 3/2x2 + 5 U(x) = x2 + 2 Calcular: 1P(x) + Q (x) = 2P(x) − U (x) = 3P(x) + R (x) = 42P(x) − R (x) = 5S(x) + T(x) + U(x) = 6S(x) − T(x) + U(x) = 4Dados los polinomios: P(x) = x4 − 2x2 − 6x − 1 Q(x) = x3 − 6x2 + 4 R(x) = 2x4 − 2x − 2 Calcular: P(x) + Q(x) − R(x) = P(x) + 2 Q(x) − R(x) = Q(x) + R(x) − P(x)= 5Multiplicar: 1(x4 − 2x2 + 2) · (x2 − 2x + 3) = 2 (3x2 − 5x) · (2x3 + 4x2 − x + 2) = 3 (2x2 − 5x + 6) · (3x4 − 5x3 − 6x2 + 4x − 3) = 6Dividir: 1(x4 − 2x3 − 11x2 + 30x − 20) : (x2 + 3x − 2) 2(x 6 + 5x4 + 3x2 − 2x) : (x2 − x + 3) 3 P(x) = x5 + 2x3 − x − 8         Q(x) = x2 − 2x + 1 7Divide por Ruffini: 1 (x3 + 2x + 70) : (x + 4) 2(x5 − 32) : (x − 2) 3 (x4 − 3x2 + 2 ) : (x −3) 8Halla el resto de las siguientes divisiones: 1(x5 − 2x2 − 3) : (x −1) 2(2x4 − 2x3 + 3x2 + 5x + 10) : (x + 2) 3 ( x4 − 3x2 + 2) :  (x − 3) 9Indica cuáles de estas divisiones son exactas: 1(x3 − 5x −1) : (x − 3) 2(x6 − 1) : (x + 1) 3(x4 − 2x3 + x2 + x − 1) : (x − 1) 4(x10 − 1024) : (x + 2) 10Comprueba que los siguientes polinomios tienen como factores los que se indican: 1(x3 − 5x −1) tiene por factor (x − 3) 2(x6 − 1) tiene por factor (x + 1) 3(x4 − 2x3 + x2 + x − 1) tiene por factor (x − 1 ) 4(x10 − 1024) tiene por factor (x + 2) 11Hallar a y b para que el polinomio x5 − ax + b sea divisible por x2 − 4. 12Determina los coeficientes de a y b para que el polinomio x3 + ax2 + bx + 5 sea divisible por x2 + x + 1. 13 Encontrar el valor de k para que al dividir 2x2 − kx + 2 por (x − 2) dé de resto 4. 14 Determinar el valor de m para que 3x2 + mx + 4 admita x = 1 como una de sus raíces. 15 Hallar un polinomio de cuarto grado que sea divisible por x2 − 4 y se anule para x = 3 y x= 5. 16 Calcular el valor de a para que el polinomio x3 − ax + 8 tenga la raíz x = −2, y calcular las otras raíces.